Application for course "Ecosystem of rabbits and foxes"
Content: Vol.rar (294.11 KB)
Uploaded: 05.09.2017
Positive responses: 0
Negative responses: 0
Sold: 1
Refunds: 0
$10
IN ARCHIVE, ONLY PROGRAM WITH SOME THEORETICAL INFORMATION IS SUBMITTED. EXPLANATORY NOTE MISSING!
Option 2.7
Consider a simple ecosystem consisting of rabbits, for which there is an unlimited supply of food, and foxes, which for food hunt for rabbits. A classical mathematical model belonging to Volterra describes this system by two nonlinear first-order equations:
dr / dt = 2r-αrf, r (0) = r0,
df / dt = -f + αrf, f (0) = f0.
Here t is the time, r = r (t) is the number of rabbits, f = f (t) is the number of foxes and α is a positive constant. At α = 0, two populations do not interact, and rabbits do what rabbits do best, and foxes die from hunger. For α> 0 foxes meet rabbits with a probability proportional to the product of the number of both. As a result of such meetings, the number of rabbits decreases, and the number of foxes (for less obvious reasons) increases.
Investigate the behavior of this system for α = 0.01 and different values of r0 and f0, ranging from 2 or 3 to several thousand. Draw the graphics of the most interesting solutions. Draw a graph with the axes r and f. Since we are silent about the units of measure, there is no reason to restrict r and f to only integer values.
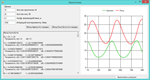
(a) Calculate the solution for r0 = 300 and f0 = 150. You should find that the behavior of the system is periodic with a period very close to 5 units of time. In other words, r (0) ≈ r (5) and f (0) ≈ f (5).
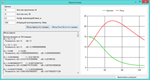
(b) Calculate the solution for r0 = 15 and f0 = 22. You should get the number of rabbits to eventually become less than 1. This can be interpreted so that rabbits die out. Find the initial conditions that doom to extinction foxes. Find the initial conditions with r0 = f0, at which both types die out.
(c) Can any component of the exact solution become negative? Can a numerical solution become negative? What will happen in this case? (In practice, the answers to the last two questions may depend on the margin of error you set.)
(d) Many modifications of this simple model have been proposed to more fully reflect what is happening in nature. For example, it is possible to prevent an unlimited increase in the number of rabbits, replacing the first equation by
dr / dt = 2 (1-r / R) r-αrf
Now even at α = 0, the number of rabbits can never exceed R. Choose some reasonable value for R and again consider some of the questions posed. In particular, what will happen with the frequency of decisions?
Option 2.7
Consider a simple ecosystem consisting of rabbits, for which there is an unlimited supply of food, and foxes, which for food hunt for rabbits. A classical mathematical model belonging to Volterra describes this system by two nonlinear first-order equations:
dr / dt = 2r-αrf, r (0) = r0,
df / dt = -f + αrf, f (0) = f0.
Here t is the time, r = r (t) is the number of rabbits, f = f (t) is the number of foxes and α is a positive constant. At α = 0, two populations do not interact, and rabbits do what rabbits do best, and foxes die from hunger. For α> 0 foxes meet rabbits with a probability proportional to the product of the number of both. As a result of such meetings, the number of rabbits decreases, and the number of foxes (for less obvious reasons) increases.
Investigate the behavior of this system for α = 0.01 and different values of r0 and f0, ranging from 2 or 3 to several thousand. Draw the graphics of the most interesting solutions. Draw a graph with the axes r and f. Since we are silent about the units of measure, there is no reason to restrict r and f to only integer values.
(a) Calculate the solution for r0 = 300 and f0 = 150. You should find that the behavior of the system is periodic with a period very close to 5 units of time. In other words, r (0) ≈ r (5) and f (0) ≈ f (5).
(b) Calculate the solution for r0 = 15 and f0 = 22. You should get the number of rabbits to eventually become less than 1. This can be interpreted so that rabbits die out. Find the initial conditions that doom to extinction foxes. Find the initial conditions with r0 = f0, at which both types die out.
(c) Can any component of the exact solution become negative? Can a numerical solution become negative? What will happen in this case? (In practice, the answers to the last two questions may depend on the margin of error you set.)
(d) Many modifications of this simple model have been proposed to more fully reflect what is happening in nature. For example, it is possible to prevent an unlimited increase in the number of rabbits, replacing the first equation by
dr / dt = 2 (1-r / R) r-αrf
Now even at α = 0, the number of rabbits can never exceed R. Choose some reasonable value for R and again consider some of the questions posed. In particular, what will happen with the frequency of decisions?
No feedback yet