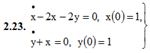ИДЗ 16.2 – Вариант 23. Решения Рябушко А.П.
Содержимое: 23v-IDZ16.2.doc (111.50 KB)
Загружен: 22.11.2022
Положительные отзывы: 0
Отрицательные отзывы: 0
Продано: 0
Возвраты: 0
90 Рублей
1. Решить операторным методом линейное дифференциальное уравнение
αẍ + βẋ + γx = f(t), x(t0) = A, ẋ(t0) = B
Функцию f(t) и значения коэффициентов α, β, γ, t0, x(t0), ẋ(t0) взять из табл. 16.4
1.23. α = 1, β = −2, γ = 1, f(t) = 1 − sint, t0 = 0, x(t0) = 0, ẋ(t0) = 0
1.23. ẍ − 2ẋ + x = 1 − sint, x(0) = 0, ẋ(0) = 0
2. Решить операторным методом систему линейных дифференциальных уравнений
Функции f1(t), f2(t) и значения ak, bk, ck, dk (k=1, 2), A, B, x(0), y(0) взять из табл. 16.5
2.23. a1 = 1, b1 = 0, c1 = −2, d1 = −2, f1(t) = 0, a2 = 0, b2 = 1, c2 = 1, d2 = 0, f2(t) = 0, x(0) = 1, y(0) = 1
αẍ + βẋ + γx = f(t), x(t0) = A, ẋ(t0) = B
Функцию f(t) и значения коэффициентов α, β, γ, t0, x(t0), ẋ(t0) взять из табл. 16.4
1.23. α = 1, β = −2, γ = 1, f(t) = 1 − sint, t0 = 0, x(t0) = 0, ẋ(t0) = 0
1.23. ẍ − 2ẋ + x = 1 − sint, x(0) = 0, ẋ(0) = 0
2. Решить операторным методом систему линейных дифференциальных уравнений
Функции f1(t), f2(t) и значения ak, bk, ck, dk (k=1, 2), A, B, x(0), y(0) взять из табл. 16.5
2.23. a1 = 1, b1 = 0, c1 = −2, d1 = −2, f1(t) = 0, a2 = 0, b2 = 1, c2 = 1, d2 = 0, f2(t) = 0, x(0) = 1, y(0) = 1
Подробное решение. Оформлено в Microsoft Word 2003 (Задание решено с использованием редактора формул)
Для удобства просмотра решений ИДЗ на смартфонах, высылается дополнительно файл в PDF-формате
Для удобства просмотра решений ИДЗ на смартфонах, высылается дополнительно файл в PDF-формате
Отзывов от покупателей не поступало