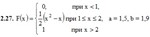ИДЗ 18.2 – Вариант 27. Решения Рябушко А.П.
Содержимое: 27v-IDZ18.2.doc (173.50 KB)
Загружен: 10.11.2016
Положительные отзывы: 0
Отрицательные отзывы: 0
Продано: 4
Возвраты: 0
140 Рублей
1. Найти закон распределения указанной дискретной CB X и ее функцию распределения F(x). Вычислить математическое ожидание M(X), дисперсию D(X) и среднее квадратичное отклонение σ(X). Построить график функции распределения F(x)
1.27. В партии из 25 изделий 6 бракованных. Для контроля их качества случайным образом отбирают четыре изделия; СВ X – число бракованных изделий среди отобранных.
2. Дана функция распределения F(х) СВ X. Найти плотность распределения вероятностей f(x), математическое ожидание М(X), дисперсию D(X) и вероятность попадания СВ X на отрезок [а; b]. Построить графики функций F(х) и f(x).
3. Решить следующие задачи.
3.27. Считается, что отклонение длины изготавливаемых деталей от стандартных является случайной величиной, распределенной по нормальному закону. Зная, что длина стандартной детали 40 см, а среднее квадратичное отклонение 0,4 см, определить, какую точность длины изделия можно гарантировать с вероятностью 0,8.
4. Решить следующие задачи.
4.27. Число солнечных дней в году для данной местности является случайной величиной, математическое ожидание которой равно 75 дням. Оценить вероятность того, что в течение года в этой местности будет более 200 солнечных дней.
1.27. В партии из 25 изделий 6 бракованных. Для контроля их качества случайным образом отбирают четыре изделия; СВ X – число бракованных изделий среди отобранных.
2. Дана функция распределения F(х) СВ X. Найти плотность распределения вероятностей f(x), математическое ожидание М(X), дисперсию D(X) и вероятность попадания СВ X на отрезок [а; b]. Построить графики функций F(х) и f(x).
3. Решить следующие задачи.
3.27. Считается, что отклонение длины изготавливаемых деталей от стандартных является случайной величиной, распределенной по нормальному закону. Зная, что длина стандартной детали 40 см, а среднее квадратичное отклонение 0,4 см, определить, какую точность длины изделия можно гарантировать с вероятностью 0,8.
4. Решить следующие задачи.
4.27. Число солнечных дней в году для данной местности является случайной величиной, математическое ожидание которой равно 75 дням. Оценить вероятность того, что в течение года в этой местности будет более 200 солнечных дней.
В задачнике в ответах могут быть опечатки. Решения задач проверялись.
Подробное решение. Оформлено в Microsoft Word 2003 (Задание решено с использованием редактора формул)
Для удобства просмотра решений ИДЗ на смартфонах, высылается дополнительно файл в PDF-формате
Подробное решение. Оформлено в Microsoft Word 2003 (Задание решено с использованием редактора формул)
Для удобства просмотра решений ИДЗ на смартфонах, высылается дополнительно файл в PDF-формате
Отзывов от покупателей не поступало