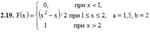ИДЗ 18.2 – Вариант 19. Решения Рябушко А.П.
Содержимое: 19v-IDZ18.2.doc (184.00 KB)
Загружен: 10.11.2016
Положительные отзывы: 0
Отрицательные отзывы: 0
Продано: 6
Возвраты: 0
140 Рублей
1. Найти закон распределения указанной дискретной CB X и ее функцию распределения F(x). Вычислить математическое ожидание M(X), дисперсию D(X) и среднее квадратичное отклонение σ(X). Построить график функции распределения F(x)
1.19. Рабочий обслуживает четыре станка. Вероятность выхода из строя в течение смены для первого станка равна 0,6, для второго – 0,5, для третьего – 0,4, для четвертого – 0,5; СВ X – число станков, вышедших из строя за смену.
2. Дана функция распределения F(х) СВ X. Найти плотность распределения вероятностей f(x), математическое ожидание М(X), дисперсию D(X) и вероятность попадания СВ X на отрезок [а; b]. Построить графики функций F(х) и f(x).
3. Решить следующие задачи.
3.19. При заданном положении точки разрыва снаряда цель оказывается накрытой пуассоновским полем осколков с плотностью λ = 2,5 осколков/м2. Площадь проекции цели на плоскость, на которой наблюдается осколочное поле, равна 0,8 м2. Каждый осколок, попавший в цель, поражает ее с полной достоверностью. Найти вероятность того, что цель будет поражена.
4. Решить следующие задачи.
4.19. Дисперсия каждой из 2500 независимых СВ не превышает 5. Оценить вероятность того, что отклонение среднего арифметического этих случайных величин от среднего арифметического их математических ожиданий не превысит 0,4.
1.19. Рабочий обслуживает четыре станка. Вероятность выхода из строя в течение смены для первого станка равна 0,6, для второго – 0,5, для третьего – 0,4, для четвертого – 0,5; СВ X – число станков, вышедших из строя за смену.
2. Дана функция распределения F(х) СВ X. Найти плотность распределения вероятностей f(x), математическое ожидание М(X), дисперсию D(X) и вероятность попадания СВ X на отрезок [а; b]. Построить графики функций F(х) и f(x).
3. Решить следующие задачи.
3.19. При заданном положении точки разрыва снаряда цель оказывается накрытой пуассоновским полем осколков с плотностью λ = 2,5 осколков/м2. Площадь проекции цели на плоскость, на которой наблюдается осколочное поле, равна 0,8 м2. Каждый осколок, попавший в цель, поражает ее с полной достоверностью. Найти вероятность того, что цель будет поражена.
4. Решить следующие задачи.
4.19. Дисперсия каждой из 2500 независимых СВ не превышает 5. Оценить вероятность того, что отклонение среднего арифметического этих случайных величин от среднего арифметического их математических ожиданий не превысит 0,4.
В задачнике в ответах могут быть опечатки. Решения задач проверялись.
Подробное решение. Оформлено в Microsoft Word 2003 (Задание решено с использованием редактора формул)
Для удобства просмотра решений ИДЗ на смартфонах, высылается дополнительно файл в PDF-формате
Подробное решение. Оформлено в Microsoft Word 2003 (Задание решено с использованием редактора формул)
Для удобства просмотра решений ИДЗ на смартфонах, высылается дополнительно файл в PDF-формате
Отзывов от покупателей не поступало