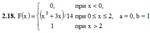DHS 18.2 - Option 18. Decisions Ryabushko AP
Content: 18v-IDZ18.2.doc (176.50 KB)
Uploaded: 10.11.2016
Positive responses: 0
Negative responses: 0
Sold: 10
Refunds: 0
$1.22
1. Find the distribution of the said discrete CB X and its distribution function F (x). Calculate the expectation M (X), the variance of D (X) and standard deviation σ (X). Draw the graph of the distribution function F (x)
1.18. In the first box 10 seals, 2 of them are defective, the second - 16, 4 of them are defective, in the third - 12 seals, including 3 defective; SW X - number of defective seals on the condition that each of the boxes taken randomly in one gland.
2. Dana distribution function F (x) DM X. Find the probability density function f (x), the expectation M (X), the variance of D (X), and the probability of hitting NE X on the interval [a; b]. Construct the graphs of the functions F (x) and f (x).
3. Solve the following problems.
3.18. The minute hand of the clock moves abruptly at the end of each minute. Find the probability that a given instant the clock shows a time which differs from the true by no more than 20 seconds.
4. Solve the following problems.
4.18. As a result, 200 independent experiments found values SW X1, X2, ..., X200 and M (X) = D (X) = 2. Rate on top of the probability that the absolute value of the difference between the arithmetic mean value of a random variable; and the expectation is less than 0.2.
1.18. In the first box 10 seals, 2 of them are defective, the second - 16, 4 of them are defective, in the third - 12 seals, including 3 defective; SW X - number of defective seals on the condition that each of the boxes taken randomly in one gland.
2. Dana distribution function F (x) DM X. Find the probability density function f (x), the expectation M (X), the variance of D (X), and the probability of hitting NE X on the interval [a; b]. Construct the graphs of the functions F (x) and f (x).
3. Solve the following problems.
3.18. The minute hand of the clock moves abruptly at the end of each minute. Find the probability that a given instant the clock shows a time which differs from the true by no more than 20 seconds.
4. Solve the following problems.
4.18. As a result, 200 independent experiments found values SW X1, X2, ..., X200 and M (X) = D (X) = 2. Rate on top of the probability that the absolute value of the difference between the arithmetic mean value of a random variable; and the expectation is less than 0.2.
Detailed solution. Decorated in Microsoft Word 2003 (Quest decided to use the formula editor)
For the convenience of viewing IDZ solutions on smartphones, an additional file in PDF format is sent
For the convenience of viewing IDZ solutions on smartphones, an additional file in PDF format is sent
No feedback yet