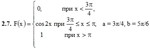DHS 18.2 - Option 7. Decisions Ryabushko AP
Content: 7v-IDZ18.2.doc (216.00 KB)
Uploaded: 10.11.2016
Positive responses: 0
Negative responses: 0
Sold: 10
Refunds: 0
$1.22
1. Find the distribution of the said discrete CB X and its distribution function F (x). Calculate the expectation M (X), the variance of D (X) and standard deviation σ (X). Draw the graph of the distribution function F (x)
1.7. The probability of hitting the target with one shot is equal to 0.8; SW X - the number of hits the target with three shots.
2. Dana distribution function F (x) DM X. Find the probability density function f (x), the expectation M (X), the variance of D (X), and the probability of hitting NE X on the interval [a; b]. Construct the graphs of the functions F (x) and f (x).
3. Solve the following problems.
3.7. The lottery played motorcycle, bicycle, and one clock. Find the expectation of winning for a person with one ticket, if the total number is 100 tickets.
4. Solve the following problems.
4.7. Produced sampling party light bulbs to determine the average length of their combustion. What should be the size of the sample to a probability not less than 0.9876, it could be argued that the average duration of the operation for the entire party has deviated from the average light bulb, resulting in a sample of not more than 10 hours, if the standard deviation of the service time bulbs h is 80?
1.7. The probability of hitting the target with one shot is equal to 0.8; SW X - the number of hits the target with three shots.
2. Dana distribution function F (x) DM X. Find the probability density function f (x), the expectation M (X), the variance of D (X), and the probability of hitting NE X on the interval [a; b]. Construct the graphs of the functions F (x) and f (x).
3. Solve the following problems.
3.7. The lottery played motorcycle, bicycle, and one clock. Find the expectation of winning for a person with one ticket, if the total number is 100 tickets.
4. Solve the following problems.
4.7. Produced sampling party light bulbs to determine the average length of their combustion. What should be the size of the sample to a probability not less than 0.9876, it could be argued that the average duration of the operation for the entire party has deviated from the average light bulb, resulting in a sample of not more than 10 hours, if the standard deviation of the service time bulbs h is 80?
Detailed solution. Decorated in Microsoft Word 2003 (Quest decided to use the formula editor)
For the convenience of viewing IDZ solutions on smartphones, an additional file in PDF format is sent
For the convenience of viewing IDZ solutions on smartphones, an additional file in PDF format is sent
No feedback yet