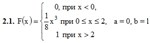DHS 18.2 - Option 1. Decisions Ryabushko AP
Content: 1v-IDZ18.2.doc (176.00 KB)
Uploaded: 10.11.2016
Positive responses: 0
Negative responses: 0
Sold: 6
Refunds: 0
$1.22
1. Find the distribution of the said discrete CB X and its distribution function F (x). Calculate the expectation M (X), the variance of D (X) and standard deviation σ (X). Draw the graph of the distribution function F (x)
1.1. The vehicle must pass on the street, which has four independently operating lights. Each traffic light at an interval of 2 minutes, takes the red and green signals; SW X - number of vehicle stops on this street.
2. Dana distribution function F (x) DM X. Find the probability density function f (x), the expectation M (X), the variance of D (X), and the probability of hitting NE X on the interval [a; b]. Construct the graphs of the functions F (x) and f (x).
3. Solve the following problems.
3.1. Roller, machine manufacturers, is considered to be the standard, if the deviation of the diameter of the size of the project does not exceed 2 mm. Random deflection roller diameters are subject to a normal distribution with standard deviation 1.6 mm, and the expectation of 0. How many standard rollers (percentage) makes the machine?
4. Solve the following problems.
4.1. To determine the quality of the products selected at random by the 2500 pieces. Among them was 50 defects. production of defective products rate is taken as an approximation of the probability of production of defective products. To determine how likely it can be ensured that the assumptions in this case the absolute error does not exceed 0.02.
1.1. The vehicle must pass on the street, which has four independently operating lights. Each traffic light at an interval of 2 minutes, takes the red and green signals; SW X - number of vehicle stops on this street.
2. Dana distribution function F (x) DM X. Find the probability density function f (x), the expectation M (X), the variance of D (X), and the probability of hitting NE X on the interval [a; b]. Construct the graphs of the functions F (x) and f (x).
3. Solve the following problems.
3.1. Roller, machine manufacturers, is considered to be the standard, if the deviation of the diameter of the size of the project does not exceed 2 mm. Random deflection roller diameters are subject to a normal distribution with standard deviation 1.6 mm, and the expectation of 0. How many standard rollers (percentage) makes the machine?
4. Solve the following problems.
4.1. To determine the quality of the products selected at random by the 2500 pieces. Among them was 50 defects. production of defective products rate is taken as an approximation of the probability of production of defective products. To determine how likely it can be ensured that the assumptions in this case the absolute error does not exceed 0.02.
Detailed solution. Decorated in Microsoft Word 2003 (Quest decided to use the formula editor)
For the convenience of viewing IDZ solutions on smartphones, an additional file in PDF format is sent
For the convenience of viewing IDZ solutions on smartphones, an additional file in PDF format is sent
No feedback yet