Solution D5-70 (Figure D5.7 condition 0 SM Targ 1988)
Content: d5-70_1988.rar (27.94 KB)
Uploaded: 26.05.2016
Positive responses: 0
Negative responses: 0
Sold: 1
Refunds: 0
Seller: Михаил_Перович
information about the seller and its items
Loyalty discount! If the total amount of your purchases from the seller more than:
| $1 | the discount is | 1% |
| $5 | the discount is | 2% |
| $10 | the discount is | 3% |
| $20 | the discount is | 5% |
| $50 | the discount is | 7% |
| $100 | the discount is | 10% |
| $200 | the discount is | 15% |
$0.49
Solution D5-70 (Figure D5.7 condition 0 SM Targ 1988)
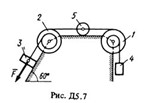
The mechanical system consists of stepped pulleys 1 and 2 with weights P1 and P2 with radii of steps R1 = R, r1 = 0,4R; R2 = R, r3 = 0,8R (the mass of each pulley is assumed to be uniformly distributed over its outer rim); loads 3, 4 and a continuous homogeneous cylindrical roller 5 with weight P3, P4, P5, respectively (Fig. D5.0-D5.9 of Table D5). The bodies of the system are connected by threads wound on pulleys; The sections of the filaments are parallel to the corresponding planes. Loads Slip on planes without friction, and rollers roll without sliding. In addition to the forces of gravity, a constant force F acts on one of the bodies of the system, and constant moments of the resistance forces act on the pulleys 1 and 2, respectively, equal to M1 and M2. Write for the given system the Lagrange equation and determine from it the quantity indicated in the table in the "Find" column, where: ε1, ε2 are the angular accelerations of pulleys 1 and 2; a3, a4, aC5 - acceleration of loads 3, 4 and the center of mass of the roller 5, respectively. When in the task it is necessary to determine ε1, ε2, consider R = 0,25 m. The one of the cargoes 3, 4 whose weight is equal to zero, is not represented in the drawing. Pulleys 1 and 2 always enter the system.
The mechanical system consists of stepped pulleys 1 and 2 with weights P1 and P2 with radii of steps R1 = R, r1 = 0,4R; R2 = R, r3 = 0,8R (the mass of each pulley is assumed to be uniformly distributed over its outer rim); loads 3, 4 and a continuous homogeneous cylindrical roller 5 with weight P3, P4, P5, respectively (Fig. D5.0-D5.9 of Table D5). The bodies of the system are connected by threads wound on pulleys; The sections of the filaments are parallel to the corresponding planes. Loads Slip on planes without friction, and rollers roll without sliding. In addition to the forces of gravity, a constant force F acts on one of the bodies of the system, and constant moments of the resistance forces act on the pulleys 1 and 2, respectively, equal to M1 and M2. Write for the given system the Lagrange equation and determine from it the quantity indicated in the table in the "Find" column, where: ε1, ε2 are the angular accelerations of pulleys 1 and 2; a3, a4, aC5 - acceleration of loads 3, 4 and the center of mass of the roller 5, respectively. When in the task it is necessary to determine ε1, ε2, consider R = 0,25 m. The one of the cargoes 3, 4 whose weight is equal to zero, is not represented in the drawing. Pulleys 1 and 2 always enter the system.
No feedback yet