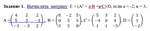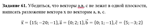TSOGU Edukon semester Mathematics 1 option 1
Content: Математика вариант 1 семестр 1.rar (459.44 KB)
Uploaded: 04.02.2016
Positive responses: 0
Negative responses: 0
Sold: 1
Refunds: 0
$1
Task 1. Calculate the matrix E = (A2 + and B + ∙ ∙ C) ∙ D, if a = 2, B = 3,
Task 11. Find the inverse of a matrix A, verify that the A-1 ∙ A = E.
Task 21. Find the solution of a system of linear equations: a) by Cramer´s rule and using the inverse matrix; b) the method of Gauss.
Task 31. Through the point M draw a direct parallel, perpendicular and at an angle of 45 to the line l. Make a drawing.
Target 41. In a triangle ABC are known coordinates of its vertices. Find the equation of the AU, the equation of height, drawn from the point B, the length of the height, angle A.
A (0, 8), B (-1, 1), C (9; 4).
Task 51. Identify the type of curve, reduce the equation to canonical form, a curve or a portion of construct.
A) 4x2 + 9u2 -16h + 5y + 61 = 0 b) at = -3√ (-2x)
Target 61. Ensure that the vectors a, b, c do not lie in one plane, write vector x by decomposition vectors a, b, c.
x ⃗ = {15; -20; -1}, a ⃗ = {0, 2, 1}, b ⃗ = {0; 1; -1}, c ⃗ = {5, -3, 2}
Task 71. The points A1, A2, A3, A4 are the top of the pyramid. Calculate:
1) The length of the edges A1A2;
2) The angle between the edges A1A2 and A3A2;
3) Grand A1A2A3
4) the volume of the pyramid;
5) The equation of the line A1A3;
6) Equation A2A3A4 plane;
7) The height of the equation, lowered from the top of A1 to the brink A2A3A4;
8) the length of this height.
Make a drawing.
A1 (1; 1; 2), A2 (2; 1; 2), A3 (1; 1; 4), A4 (6; -3, 8).
Task 81. Given the complex numbers z1 and z2 in algebraic form. Record them in the trigonometric and exponential form and portray the complex plane. Proceed: z1 + z2, z1z2, z1: z2, z23. Find all the roots of 3 -z1 = 0, to represent them on the plane.
z1 = 1 - √3 i, z2 = - i
Task 11. Find the inverse of a matrix A, verify that the A-1 ∙ A = E.
Task 21. Find the solution of a system of linear equations: a) by Cramer´s rule and using the inverse matrix; b) the method of Gauss.
Task 31. Through the point M draw a direct parallel, perpendicular and at an angle of 45 to the line l. Make a drawing.
Target 41. In a triangle ABC are known coordinates of its vertices. Find the equation of the AU, the equation of height, drawn from the point B, the length of the height, angle A.
A (0, 8), B (-1, 1), C (9; 4).
Task 51. Identify the type of curve, reduce the equation to canonical form, a curve or a portion of construct.
A) 4x2 + 9u2 -16h + 5y + 61 = 0 b) at = -3√ (-2x)
Target 61. Ensure that the vectors a, b, c do not lie in one plane, write vector x by decomposition vectors a, b, c.
x ⃗ = {15; -20; -1}, a ⃗ = {0, 2, 1}, b ⃗ = {0; 1; -1}, c ⃗ = {5, -3, 2}
Task 71. The points A1, A2, A3, A4 are the top of the pyramid. Calculate:
1) The length of the edges A1A2;
2) The angle between the edges A1A2 and A3A2;
3) Grand A1A2A3
4) the volume of the pyramid;
5) The equation of the line A1A3;
6) Equation A2A3A4 plane;
7) The height of the equation, lowered from the top of A1 to the brink A2A3A4;
8) the length of this height.
Make a drawing.
A1 (1; 1; 2), A2 (2; 1; 2), A3 (1; 1; 4), A4 (6; -3, 8).
Task 81. Given the complex numbers z1 and z2 in algebraic form. Record them in the trigonometric and exponential form and portray the complex plane. Proceed: z1 + z2, z1z2, z1: z2, z23. Find all the roots of 3 -z1 = 0, to represent them on the plane.
z1 = 1 - √3 i, z2 = - i
No feedback yet